Analyse de Fourier sur l’index
Dans le post précédent nous avons vu que la théorie des fonctions intégrables n’est pas suffisante pour définir la transformée de Fourier pour des fonctions simples comme \(\cos(t)\) ou \(\sin(t)\). On va voir rapidement dans cette note comment élargir la théorie à des objets plus généraux. On verra que cela passe par la notion de distribution temperée qui est étoitement liée à la notion de mesure que l’on détaillera par la suite.
Sommaire
1. Distributions tempérées
La théorie de Fourier peut s’étendre à des objets qu’on appelle les distributions. Cette théorie a été développée par Schwartz dans les années 50 et généralise en quelque sorte la notion de fonction.
De la fonction aux distributions
L’idée de base de cette théorie est qu’une fonction n’est plus vue comme étant le procédé “à un point j’associe une valeur” mais plutôt comme une étant le processus “j’associe une valeur moyenne autour d’un point donné.”
Cette approche permet de lisser les irrégularités de la fonction de base et définit de façon plus “concrète” la notion de fonction. En effet, dans la vraie vie (celle de la physique), lorsqu’on veut mesurer une fonction on dispose de capteurs imparfaits qui mesurent une valeur locale et moyennée de la fonction.
Prenons l’exemple de la température d’une pièce. On cherche à l’aide d’un capteur de température à déterminer en un point de la pièce \(x_0\), par définition infinitésimal, la valeur \(\phi(x_0)\) de cette température. A cause des imperfections du capteur la valeur du mesurée sera plutôt une valeur moyenne de la température autour du point en question. On aura donc plutôt accès à quelque chose comme \(\frac{1}{\text{vol}(D)}\int_{D \subset \mathbb{R^{3}}} \phi(x) dx\) avec \(\text{vol}(D)\) le volume de la région \(D\) autour du point \(x_0\). On peut réécrire cette expression comme \(T_f(\phi)=\int_{\mathbb{R^{3}}} f(x) \phi(x)dx\) où \(f(x)=\frac{1}{\text{vol}(D)}\) si \(x \in D\) (le point x est dans la région du capteur) et \(0\) ailleurs. \(f\) représente en quelque sorte la “qualité” de notre capteur. Pour un capteur infiniment précis on aurait \(f(x)=1\) si \(x=x_0\) et \(0\) ailleurs et dans ce cas \(T_f(\phi)=\phi(x_0)\). En évaluant en chaque point avec ce capteur infiniment précis on aurait alors accès à la fonction température \(\phi\) en tout point de l’espace. Cette considération est la base de la notion de distribution.
La transformée de Fourier dans ce cadre ne sera plus une notion liée aux fonctions mais sera une notion liée aux distributions c’est à dire à un certain type d’objets qui à une fonction \(\phi\) donné associe une valeur représentant une moyenne locale de notre fonction \(\phi\).
Espace de Schwartz
Pour définir la transformée de Fourier dans ce contexte on va se restreindre à certains types de fonctions \(\phi\) qu’on va pouvoir “mesurer” à l’aide de notre “capteur” \(f\). Ces fonctions particulières seront appelées fonctions de l’espace de Schwarz.
Pour définir cet espace de fonctions on introduit la notion de décroissance rapide et croissance lente d’une fonction:
Définition (Décroissance rapide et croissance lente) Une fonction \(\phi: \mathbb{R} \rightarrow \mathbb{C}\) est dite à décroissance rapide si: \[\begin{equation} \forall n\in \mathbb{N}, \exists C_n\geq0, \lvert \phi(x) \rvert \leq \frac{C_n}{(1+ x^{2})^{n}} \text{ pour tout x} \end{equation}\]
Une fonction est dite à croissance lente si:
\[\begin{equation} \forall n\in \mathbb{N}, \exists C_n\geq0, \lvert \phi(x) \rvert \leq C_n(1+ x^{2})^{n} \text{ pour tout x} \end{equation}\]
Autrement dit une fonction à décroissance rapide décroit plus vite que tout inverse de tout polynôme et de la même manière une fonction à croissance lente croît moins vite que n’importe quel polynôme.
Par exemple la fonction \(x\rightarrow e^{-\lvert x\rvert}\) est à décroissance rapide. Toute fonction à support compact (c’est à dire nulle en dehors d’un intervalle bornée) est aussi à décroissance rapide. De la même manière toute fonction bornée est à croissance lente.
On va aussi ajouter une hypothèse de régularité aux fonctions \(\phi\): les fonctions \(\phi\) admissibles seront des fonctions indéfiniment dérivables dont chaque dérivée est à décroissance rapide.
Définition (Fonction test et Espace de Schwartz) On appelle fonction test une fonction \(\phi: \mathbb{R} \rightarrow \mathbb{C}\) infiniment différentiable dont toutes les dérivées décroissent rapidement. Plus précisément si \(\phi^{(n)}\) est la dérivée \(n\)-ième de \(\phi\) on a: \[\begin{equation} \forall k,n \in \mathbb{N}^{2}, \sup_{x\in \mathbb{R}} \lvert x^{k} \phi^{(n)}(x)\rvert < +\infty \end{equation}\]
Dans la littérature on peut aussi trouver les conditions suivantes:
\[\begin{equation} \forall k,n \in \mathbb{N}^{2} \text{ } \lim_{x \rightarrow \pm\infty} \lvert x^{k} \phi^{(n)}(x)\rvert=0 \end{equation}\]
\[\begin{equation} \forall k,n \in \mathbb{N}^{2}, \exists C_{n,k}\geq 0 \text{ } \lvert x^{k} \phi^{(n)}(x)\rvert \leq \frac{C_{n,k}}{1+ x^{2}} \text{ for all x} \end{equation}\]
On note \(S(\mathbb{R})\) l’ensemble des fonctions tests. Cet ensemble s’appelle l’espace de Schwartz.
On peut voir facilement par (5) que les fonctions de l’espace de Schwartz sont intégrables sur \(\mathbb{R}\). De plus toute combinaison linéaire de fonctions de l’espace de Schwartz est de Schwartz.
Les fonctions \(C^{\infty}\) à support compact sont des fonctions de l’espace de Schwartz, tout comme les fonction du type \(P(x)e^{-x^{2}}\) avec \(P(x)\) un polynôme. En particulier la gaussienne \(t\rightarrow e^{-t^{2}}\) est dans l’espace de Schwartz. La figure ci dessous représente cette fonction ainsi que ses deux premières dérivées en rouge bleu et vert. En noir la fonction créneau qui est à décroissance rapide mais qui n’est pas infiniment dérivable et donc qui n’appartient pas à l’espace de Schwartz.
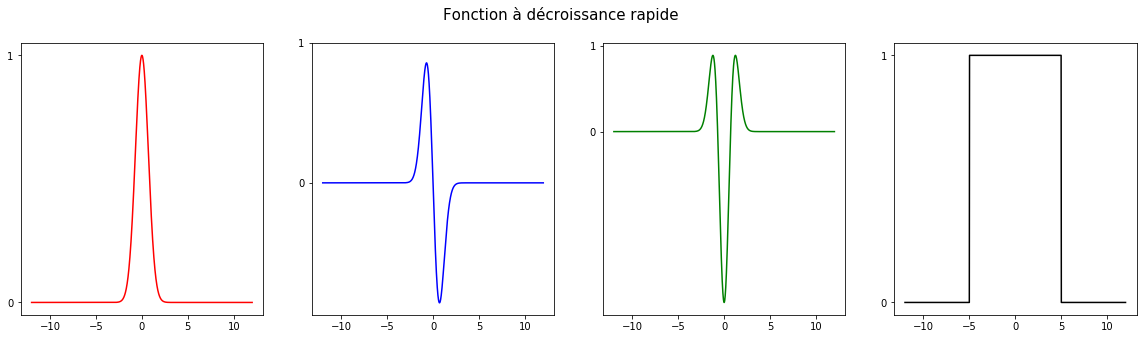
La régularité des fonctions de l’espace de Schwartz vont nous permettre d’avoir de bonnes propriétés pour définir la transformée de Fourier des distributions.
Remarque 1. Les conditions (3), (4) et (5) sont bien équivalentes. En effet si les fonctions vérifient (3) alors on va utiliser l’astuce \(\frac{\lvert x \rvert^{k}+\lvert x \rvert^{k+2}}{1+\lvert x\rvert^{2}}=\lvert x \rvert^{k}\). Ainsi \(\lvert x^{k} \phi^{(n)}(x) \rvert = \lvert x\rvert^{k} \lvert \phi^{(n)}(x) \rvert=\frac{\lvert x \rvert^{k}+\lvert x \rvert^{k+2}}{1+\lvert x\rvert^{2}} \lvert \phi^{(n)}(x) \rvert\). Donc \(\lvert x^{k} \phi^{(n)}(x) \rvert \leq \frac{\lvert x \rvert^{k} \lvert \phi^{(n)}(x) \rvert+\lvert x \rvert^{k+2} \lvert \phi^{(n)}(x) \rvert}{1+\lvert x\rvert^{2}}\). Cependant comme le sup de \(x \rightarrow \lvert x\rvert^{k} \lvert \phi^{(n)}(x)\rvert\) est fini par (3) on peut majorer par une constante \(C_{n,k}\) sur \(\mathbb{R}\) et idem pour \(x \rightarrow \lvert x\rvert^{k+2} \lvert \phi^{(n)}(x)\rvert\) par une constante \(C_{n,k+2}\) de sorte qu’on ait (5). Inversement (5) implique (3) de manière directe car \(\frac{1}{1+x^{2}}\leq 1\). En conclusion (3) est équivalent à (5). De plus on peut voir facilement que (4) implique (3) car dans ce cas \(x^{k} \phi^{(n)}(x)\) est aussi petite que l’on veut au voisinage de l’infini et par continuité elle est bornée pour tout intervalle fermé, donc le sup est fini. Plus précisément si on suppose (4) alors pour \(\epsilon >0\) il existe \(x_0\) tel que pour \(x\geq x_0\) \(\lvert x^{k} \phi^{(n)}(x) \rvert< \epsilon\). Donc \(\sup_{x > x_0} \lvert x^{k} \phi^{(n)}(x)\rvert < +\infty\). De plus \(x\rightarrow \lvert x^{k} \phi^{(n)}(x)\rvert\) est continue, donc bornée sur \([0,x_0]\) et donc \(\sup_{x \in [0,x_0]} \lvert x^{k} \phi^{(n)}(x)\rvert < +\infty\). On peut faire le même raisonnement pour \(x<0\) pour déduire la propriété pour tout \(x\). Enfin il est clair que (5) implique (4).
\(S(\mathbb{R})\) est un espace de fonction dans lequel on peut définir une notion de continuité propres aux fonctions de l’espace de Schwartz qui nous sera utile pour la suite.
Définition (Continuité dans l’espace de Schwartz) On dit qu’une suite \((\phi_m)\_m\) converge dans l’espace de Schwartz vers \(\phi\) si pour tout \(n,k\in \mathbb{N}^{2}\) la suite \((x\rightarrow x^{k}\phi_{m}^{(n)}(x))_m\) converge uniformément vers \(x\rightarrow x^{k}\phi^{(n)}(x)\). Autrement dit si: \[\begin{equation} \forall n,k\in \mathbb{N}^{2} \text{ } \lim_{m\rightarrow +\infty} \sup_{x \in \mathbb{R}} \lvert x^{k} (\phi_{m}^{(n)}(x) - \phi^{(n)}(x)) \rvert=0 \end{equation}\]
On note cette relation \(\phi_m \rightarrow_{m\rightarrow +\infty} \phi\)
Distribution tempérée
Ces fonctions tests permettent de définir de manière très générale une distribution tempérée comme étant le procédé qui à une fonction test de l’espace de Schwartz associe une valeur scalaire. Plus précisément:
Définition (Distribution tempérée) Une distribution tempérée est une fonction \(T: S(\mathbb{R}) \rightarrow \mathbb{R}\) continue et linéaire. C’est à dire \(T(a.\phi_1+b.\phi_2) =a.T(\phi_1)+b.T(\phi_2)\) et si \(\phi_m \rightarrow_{m\rightarrow +\infty} \phi\) alors \(T(\phi_m) \rightarrow_{m\rightarrow +\infty} T(\phi)\) dans \(\mathbb{R}\).
Autrement dit une distribution tempérée est une fonction linéaire et continue d’un espace de fonctions vers \(\mathbb{R}\). On parle de distribution tempérée car la croissance de la distribution est tempérée par la décroissance rapide de la fonction test.
L’idée centrale des distributions tempérée est qu’on peut voir n’importe quelle fonction un peu régulière \(f\) comme une distribution. On parle ici de distribution tempérée associée à f:
Définition (Distribution tempérée associée à f) Soit \(f\) une fonction intégrable localement et à croissance lente. On définit la distribution tempérée associée à \(f\) comme étant l’application \(T_f: S(\mathbb{R}) \rightarrow \mathbb{R}\) qui à \(\phi\) associe le scalaire:
\[\begin{equation} T_f(\phi)=\int_{\mathbb{R}} f(x) \phi(x)dx \end{equation}\]
On note souvent \(T_f(\phi)=\langle f, \phi \rangle\) comme cela ressemble à un produit scalaire. De plus il arrive dans la littérature qu’on note \(T_f\) simplement par \(f\), c’est à dire qu’on identifie fonction et distribution. On remarque que les fonctions \(f\) admissibles ont des hypothèses de régularité assez faibles: il suffit qu’elles soient localement intégrables et qu’elles ne croissent pas trop vite. Si on revient à nos fonctions \(x \rightarrow e^{i n \omega x}\) ou encore \(cos(x),sin(x)\) on voit bien qu’elles vérifient ces conditions car elles sont bornées par \(1\).
Remarque 2. Cette intégrale est bien définie. En effet comme \(f\) est localement intégrable sur n’importe quel intervalle fermé et que \(\phi\) est continue alors la fonction \(x\rightarrow f(x)\phi(x)\) est intégrable sur n’importe quel intervalle fermé. Le problème se trouve donc à l’infini mais comme la fonction \(\phi\) appartient à l’espace de Schwartz et que \(f\) est à croissance lente l’intégrale est donc finie. Plus précisément il existe des constantes \(C(f),C(\phi)\) tels que \(\lvert f(x) \rvert \leq C(1+x^2)\) et \(\lvert \phi(x) \rvert \leq \frac{C(\phi)}{(1+x^2)^{2}}\) pour tout \(x\). On peut donc conclure que pour tout \(x\), \(\lvert f(x) \phi(x) \rvert \leq \frac{C(f)C(\phi)}{1+x^{2}}\) qui est le terme d’une intégrale convergente sur \(\mathbb{R}\).
Remarque 3. Une distribution tempérée définit bien une distribution. Elle est clairement linéaire en \(\phi\) et elle est bien continue en \(\phi\). En effet si \(\phi_m \rightarrow \phi\) et \(I_m=\lvert T_f(\phi_m)-T_f(\phi) \rvert\) alors \(I_m\leq \int_{\mathbb{R}} \lvert f(x) \rvert \lvert \phi_m(x)-\phi(x) \rvert dx\). Soit \(N\geq 2\) on a \(1=(1+x^{2})^{N} (1+x^{2})^{-N}\) ce qui implique : \[\begin{equation} I_m\leq \int_{\mathbb{R}}(1+x^{2})^{N} (1+x^{2})^{-N} \lvert f(x) \rvert \lvert \phi_m(x)-\phi(x) \rvert dx \end{equation}\] Comme \(f\) est à croissance lente \(x \rightarrow (1+x^{2})^{N} \lvert f(x) \rvert\) est borné par une certaine constante \(C(f)\). Aussi: \[\begin{equation} I_m\leq C(f) \int_{\mathbb{R}}(1+x^{2})^{-N+1} (1+x^{2})^{-1}\lvert \phi_m(x)-\phi(x) \rvert dx \end{equation}\] De plus par combinaison linéaire \(\phi_m-\phi\) est aussi de Schwartz ce qui implique: \[\begin{equation} I_m\leq C(f) \sup_{x\in \mathbb{R}} \lvert (1+x^{2})^{-N+1}(\phi_m(x)-\phi(x)) \rvert \int_{\mathbb{R}} (1+x^{2})^{-1} dx \end{equation}\] On a \(\int_{\mathbb{R}} \frac{1}{1+x^{2}} dx < \infty\) et donc en faisant tendre \(m \rightarrow +\infty\) dans l’expression précédente on a: \[\begin{equation} \lim_{m \rightarrow +\infty} I_m\leq C(f) \int_{\mathbb{R}} (1+x^{2})^{-1} dx \lim_{m \rightarrow +\infty} \sup_{x\in \mathbb{R}} \lvert (1+x^{2})^{-N+1}(\phi_m(x)-\phi(x)) \rvert \end{equation}\] Le membre de droite tend vers \(0\) par définition de \(\phi_m \rightarrow \phi\) on a donc \(I_m \rightarrow 0\) ce qui prouve la continuité.
Remarque 4. Cette représentation est unique. On peut effectivement vérifier que si \(T_{f_1}(\phi)=T_{f_2}(\phi)\) pour tout \(\phi\) alors \(f_1=f_2\). C’est pour cette raison qu’on peut parler de “la” distribution associée à \(f\).
On voit ici apparaître une ébauche de définiton de la transformée de Fourier d’une distribution tempérée associée à \(f\). En effet en “déplaçant” la notion de transformée de Fourier de \(f\) sur les fonctions tests \(\phi\) (qui sont intégrables et donc pour lesquelles la transformée de Fourier existe) on va pouvoir la définir pour des classes de fonctions plus générales que les fonctions intégrables.
2. La transformée de Fourier des distributions tempérées
Par la suite, pour un fonction intégrable \(\phi\), on notera \(\widehat{\phi}\) la transformée de Fourier de \(\phi\) au sens des fonctions.
De la même manière que la transformée de Fourier d’une fonction était une fonction la transformée de Fourier d’une distribution tempérée est une distribution tempérée.
Définition (Transformée de Fourier d’une distribution tempérée associée à \(f\)) On appelle transformée de Fourier d’une distribution tempérée associée à une fonction \(f\) localement intégrable et à croissance lente la distribution tempérée \(\mathcal{F}(T_f)\) définie par:
\[\begin{equation} \phi \in S(\mathbb{R}) \rightarrow \int_{\mathbb{R}} f(x) \widehat{\phi}(x) dx \end{equation}\]
Beaucoup de questions se posent: l’intégrale définit plus haut existe-t-elle ? est-ce qu’on définit bien une distribution ? Comment la calculer ?
Existence
D’après les résultats précédents il suffit que \(\widehat{\phi}\) soit aussi de Schwartz pour que l’intégrale existe. On peut donner un sens à cet intégrale en utilisant le résultat suivant:
Une fonction test est de Schwartz si et seulement si sa transformée de Fourier est de Schwartz. Autrement dit, \(\phi \in S(\mathbb{R})\) si et seulement si \(\widehat{\phi} \in S(\mathbb{R})\).
On peut donner une rapide esquisse de ce théorème. On peut prouver que \(\phi \in S(\mathbb{R})\) si et seulement si \(\lim_{x \rightarrow \pm \infty} \frac{d^{n}}{dx^{n}} x^{k} \phi(x)=0\) pour tout \(n,k \in \mathbb{N}^{2}\). Or on sait par les règles de calculs que la transformée de Fourier de \(x \rightarrow (-2i\pi x)^{k} \phi^{(n)}(x)\) est \(x \rightarrow \frac{d^{k}}{dx^{k}} (2i\pi x)^{n} \widehat{\phi}(x)\). De plus on sait que pour une fonction intégrable sa transformée de Fourier tend vers \(0\) à l’infini (lemme de Riemann-Lebesgue). Or \(x \rightarrow (-2i\pi x)^{k} \phi^{(n)}(x)\) est de Schwartz donc intégrable aussi en utilisant Riemann-Lebesgue \(\lim_{x \rightarrow \pm \infty} \frac{d^{n}}{dx^{n}} x^{k} \widehat{\phi}(x)=0\) ce qui prouve que \(\widehat{\phi} \in S(\mathbb{R})\) si \(\phi \in S(\mathbb{R})\). Pour l’implication opposée on applique le même argument en utilisant la transformée de Fourier inverse.
Ce théorème nous prouve que l’intégrale définit équation (12) est bien définie car \(f\) est localement intégrable et à croissance lente et \(\phi \in S(\mathbb{R})\). Il a d’autres implications fortes pour l’étude des transformées de Fourier de fonctions de l’espace de Schwartz. Dans le cas général la transformée de Fourier inverse d’une fonction intégrable n’est pas forcément égale à la fonction: ceci n’est vrai aux points où la fonction est continue. Or grâce au théorème précédent les fonctions de l’espace de Schwartz n’ont pas ce problème et on peut inverser la transformée de Fourier partout.
\(\mathcal{F}(T_f)\) définit une distribution tempérée
Comme dit précédemment la transformée de Fourier d’une distribution tempérée est une distribution tempérée. La linéarité est claire grâce à la linéarité de la transformée de Fourier des fonctions. Il nous manque la continuité qui est vérifiée grâce au résultat suivant:
Considérons \((\phi_n)_n\) une suite de \(S(\mathbb{R})\). On a:
\[\begin{equation} \phi_n \rightarrow_{n\rightarrow \infty} \phi \iff \widehat{\phi_n} \rightarrow_{n\rightarrow \infty} \widehat{\phi} \end{equation}\]
La preuve de ce théorème utilise les mêmes idées que pour lé théorème précédent. Le lecteur peut se référer à la Proposition 19.2.5 dans [1] pour plus de détails. Ce théorème nous permet de montrer la continuité de \(\mathcal{F}(T_f)\). Pour cela on peut par exemple utiliser le même raisonnement que dans la remarque 3 en remplaçant les \(\phi\) par des \(\widehat{\phi}\) qui sont aussi de Schwartz.
En conclusion la transformée de Fourier d’une distribution tempérée associée à \(f\) est bien une distribution tempérée.
Remarque 5. On peut définir de manière plus générale la transformée de Fourier d’une distribution tempérée pas nécessairement associée à une fonction \(f\) comme étant la distribution tempérée définie par \(\mathcal{F}(T)(\phi)=T(\widehat{\phi})\).
Comment calculer \(\mathcal{F}(T_f)\) ?
A la différence de la transformée de Fourier des fonctions la transformée de Fourier d’une distribution tempérée est définie de manière implicite. Dans le cas d’une fonction intégrable \(f\) on avait la formule \(\hat{f}(x)=\int_{\mathbb{R}} f(t)e^{-ixt} dt\) alors que dans ce cas présent on a l’impression qu’il faut faire le calcul pour tout \(\phi\). Le résultat suivant va nous aider un peu:
Si \(f \in L^{1}(\mathbb{R})\) ou \(L^{2}(\mathbb{R})\) (f est intégrable ou de carré intégrable sur \(\mathbb{R}\)). Alors \(\mathcal{F}(T_f)=T_{\widehat{f}}\)
Ce résultat nous dit que dans le cas des fonctions intégrables il suffit de calculer la transformée de Fourier de \(f\) pour avoir accès à la transformée de Fourier de sa distribution. Il se prouve facilement en utilisant Fubini. Il n’est cependant pas vrai dans le cas général des fonctions \(f\) localement intégrables et à croissance lente.
Une manière pratique de calculer ces transformées de Fourier est d’utiliser les notions de dérivations des distributions tempérées. On a effectivement vu qu’une distribution est en quelque sorte une “fonction” généralisée. On peut définir la dérivée d’une distribution tempérée en “déplaçant” la dérivée sur les fonctions tests de la même manière que pour la définition de sa transformée de Fourier. La distribution dérivée \(T'\) est définie comme \(T'(\phi)=-T(\phi')\). Cette notion est utile pour le calcul des transformées de Fourier des distributions car elle permet de trouver des équations aux dérivées partielles simples dont nos transformées de Fourier sont solutions. En résolvant ces équations on peut trouver facilement une expression de ces transformées de Fourier.
On peut calculer cependant quelques cas faciles et utiles en pratiques.
Cas de la distribution \(\delta\). On considère pour \(a\in \mathbb{R}\) la fonction \(f_{a}(x)=1\) si \(x=a\) et \(0\) sinon. Cette fonction correspond à notre capteur de précision infinie de l’introduction. C’est bien une fonction localement intégrable et à croissance lente. Sa distribution tempérée associée est la \(T_{f_{a}}(\phi)=\int_{\mathbb{R}} f_{a}(x) \phi(x)dx=\phi(a)\) pour tout \(\phi \in S(\mathbb{R})\). On note cette distribution \(\delta_{a}\), elle s’appelle la distribution de dirac en \(a\). Sa transformée de Fourier est la distribution \(\mathcal{F}(\delta_{a})(\phi)=\int_{\mathbb{R}}f_{a}(x) \widehat{\phi}(x)dx=\widehat{\phi}(a)=\int_{\mathbb{R}} e^{-2 i\pi a x} \phi(x) dx\). On a donc \(\langle \delta_{a}, \phi\rangle=\langle T_{g_a}, \phi \rangle\) où \(g_a: x\rightarrow e^{-2i \pi ax}\). Ainsi \(\mathcal{F}(\delta_a)=T_{g_a}\) ce qu’on écrit de manière moins formelle \(\widehat{\delta_a}(x)=e^{-2i\pi ax}\).
Cas de la fonction \(x \rightarrow e^{2i\pi ax}\). Cette fonction est la base des fonctions périodiques. Pour \(a \in \mathbb{R}\) la fonction \(f_a: x\rightarrow e^{2i \pi ax}\) est bien localement intégrable et à croissance lente car bornée par \(1\). Elle définit donc une distribution tempérée \(T_f\). On a par définition: \(\langle F(T_f), \phi \rangle= \langle T_f, \widehat{\phi} \rangle=\int_{\mathbb{R}}e^{2i \pi ax} \widehat{\phi}(x)dx\). On remarque que cette expression est égale à \(\mathcal{F}^{-1}(\widehat{\phi})(a)=\phi(a)\) car \(\phi\) est de Schwartz. D’où \(\langle \mathcal{F}(T_f), \phi \rangle=\langle \delta_{a}, \phi \rangle\). On peut l’écrire de manière un peut moins formelle \(\widehat{e^{2i\pi ax}}=\delta_{a}\) qu’il faut lire comme “la transformée de Fourier de la distribution tempérée associée à la fonction \(x\rightarrow e^{2i\pi ax}\) est la distribution tempérée dirac en \(a\).” En prenant \(a=0\) on trouve l’expression de la transformée de Fourier de la distribution tempérée associée à la fonction constante égale à \(1\): \(\widehat{1}=\delta_{0}\)
Application: la transformée de Fourier des signaux périodiques réguliers
Reprenons l’exemple du post précédent dans lequel on voulait lier les séries de Fourier et la transformée de Fourier. On considère un signal périodique \(f\) de période \(T\) qui peut s’écrire sous la forme de sa série de Fourier \(f(t)=\sum_{n\in \mathbb{Z}} c_n(f) e^{\frac{2i \pi n t}{T}}\).
On peut prouver que le signal définit bien une distribution tempérée \(T_f\) (voir par exemple Proposition 36.1.3 dans [1]). Ainsi par linéarité de la transformée de Fourier et l’exemple précédent on a: \[\begin{equation} \mathcal{F}(T_f)=\sum_{n\in \mathbb{Z}} c_n(f) \mathcal{F}(T_{t\rightarrow e^{\frac{2 i\pi n t}{T}}})=\sum_{n\in \mathbb{Z}} c_n(f) \delta_{\frac{n}{T}} \end{equation}\] On peut donc définir la transformée de Fourier d’un signal périodique au sens des distribution. On peut la représenter comme une infinité de “pics” de valeurs les coefficients de Fourier du signal aux fréquences \(\frac{n}{T}\).
3. Conclusion
Dans ce post j’ai rapidement abordé la notion de distribution tempérée qui généralise en quelque sorte les fonctions. Ces objets permettent de définir de manière assez générale une transformée de Fourier. On remarque en regardant l’équation (7) que ces objets sont assez proches des mesures de la théorie de Lebesgue. En effet si on considère dans l’équation (7) la mesure de densité \(fd\lambda\) avec \(\lambda\) la mesure de Lebesgue sur \(\mathbb{R}\) on retombe sur l’intégrale de \(\phi\) selon cette mesure. Plus généralement toutes les mesures finies peuvent définir une distribution. On peut définir la transformée de Fourier d’une mesure finie sur \(\mathbb{R}\) comme étant:
Définition (Mesures finies et transformée de Fourier) On définit l’espace des mesures positives finies, et on le note \(\mathcal{M}_{+}(\mathbb{R})\), comme l’ensemble des mesures \(\mu\) positives telles que \(\mu(\mathbb{R})<+\infty\). Pour \(\mu \in \mathcal{M}_{+}(\mathbb{R})\) on définit sa transformée de Fourier comme: \[\begin{equation} \mathcal{F}(\mu)(\nu)=\int_{\mathbb{R}} e^{-2i\pi \nu x}d\mu(x) \end{equation}\]
L’objectif de la note suivante sera d’étudier cet objet et de faire le lien avec celui présenté ici (quelles différences, quels points communs ?).
Références
[1] Claude Gasquet and Patrick Witomski, Fourier analysis and applications. Filtering, numerical computation, wavelets. Texts in Applied Mathematics. 1999.